A recent Science paper entitled Negative Absolute Temperature for Motional Degrees of Freedom has generated a lot of discussion on the blogosphere (example) already. This post is about the equations behind the concept of negative temperature. The discussion and figure is taken out of chapter 12 of the excellent book Thermodynamic Driving Forces by Dill and Bromberg.
The thermodynamic definition of temperature is
$$dS=\frac{dU}{T}=\left(\frac{dS}{dU}\right)_{V,N}dU\Rightarrow\frac{1}{T}=\left(\frac{dS}{dU}\right)_{V,N}$$while the statistical mechanical definition of entropy is $$S=k\ln(W)$$
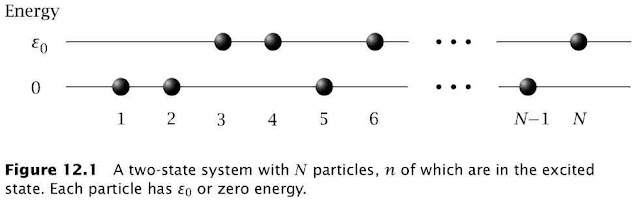
For a two-state system (Figure 12.1)$$\frac{1}{T}=k\left(\frac{d\ln(W)}{dn}\right)_{V,N} \left(\frac{dn}{dU}\right)$$The multiplicity term can be rewritten as $$\ln(W)=\ln\left(\frac{N!}{n!(N-n)!}\right)\approx-n\ln\left(\frac{n}{N}\right)-(N-n)\ln\left(\frac{N-n}{N}\right)$$where the last term used Stirling's approximation $x!\approx (x/e)^x$. The internal energy is given by$$U=n\varepsilon_0\Rightarrow\frac{dn}{dU}=\frac{1}{\varepsilon_0}$$so $T$ can be defined in terms of the fraction of molecules in the ground $(f_{ground}=n/N)$ and excited state $(f_{excited}=1-n/N)$ $$\frac{1}{T}=\frac{k}{\varepsilon_0}\ln\left(\frac{f_{ground}}{f_{excited}}\right) $$At equilibrium these fractions are determined by the Boltzmann distribution$$\frac{f_{ground}}{f_{excited}}=e^{\varepsilon_0/kT}>1$$This is the $T$ you measure with a thermometer and this $T$ can never be negative at equilibrium. However, if you create a excited macrostate for which $f_{ground}/f_{excited}<1$ then the corresponding variable $T$ can indeed be negative. As pointed out by Michael de Podesta this happens all the time in a laser.

This work (except the first figure which is © by Garland Science) is licensed under a Creative Commons Attribution 3.0 Unported License.
The thermodynamic definition of temperature is
$$dS=\frac{dU}{T}=\left(\frac{dS}{dU}\right)_{V,N}dU\Rightarrow\frac{1}{T}=\left(\frac{dS}{dU}\right)_{V,N}$$while the statistical mechanical definition of entropy is $$S=k\ln(W)$$
For a two-state system (Figure 12.1)$$\frac{1}{T}=k\left(\frac{d\ln(W)}{dn}\right)_{V,N} \left(\frac{dn}{dU}\right)$$The multiplicity term can be rewritten as $$\ln(W)=\ln\left(\frac{N!}{n!(N-n)!}\right)\approx-n\ln\left(\frac{n}{N}\right)-(N-n)\ln\left(\frac{N-n}{N}\right)$$where the last term used Stirling's approximation $x!\approx (x/e)^x$. The internal energy is given by$$U=n\varepsilon_0\Rightarrow\frac{dn}{dU}=\frac{1}{\varepsilon_0}$$so $T$ can be defined in terms of the fraction of molecules in the ground $(f_{ground}=n/N)$ and excited state $(f_{excited}=1-n/N)$ $$\frac{1}{T}=\frac{k}{\varepsilon_0}\ln\left(\frac{f_{ground}}{f_{excited}}\right) $$At equilibrium these fractions are determined by the Boltzmann distribution$$\frac{f_{ground}}{f_{excited}}=e^{\varepsilon_0/kT}>1$$This is the $T$ you measure with a thermometer and this $T$ can never be negative at equilibrium. However, if you create a excited macrostate for which $f_{ground}/f_{excited}<1$ then the corresponding variable $T$ can indeed be negative. As pointed out by Michael de Podesta this happens all the time in a laser.

This work (except the first figure which is © by Garland Science) is licensed under a Creative Commons Attribution 3.0 Unported License.
No comments:
Post a Comment