Peer instruction question on enthalpy

Is this an endo- or exothermic process?

         

Where to submit your research paper?

Jeremy Fox wrote an interesting blog post, which in turn has sparked at least two others (here and here).  Here are my thoughts on the issues that were raised, though taken in a different order, plus a few extra questions at the end.

Aim as high as you reasonably can.  As I read it the main point made in the original post is: don't waste time submitting to journals where the paper has very little chance of getting accepted.  I agree with this.

I've come to the opinion that for me (a computational chemist) the journal landscape has three tiers:
1. Science and Nature (I have never submitted a paper there)
2. Journals with an impact factor greater than roughly 10 (PNAS, JACS, etc).  (I submit once in a blue moon.)
3. Everything else.  (This is were the vast majority of my papers go).

Is it a society journal?  For Tier 3 journals my preferences are PLoS ONE >> society journals > commercial publishers (with Elsevier dead last).

I'm not particularly excitable but the Research Work Act really "brought my pis to a boil" as they say here in Denmark.  The RWA made me realize that commercial publishers (who lobbied hard for this piece of ... legislation) view my papers as their property (which it is once you sign away your copyright!) and are willing to actively hurt science to increase their already obscene profits.  So I joined the Elsevier boycott.

However, it is worth remembering that the RWA was "applauded" by the Association of American Publishers which includes societies such as the ACS and AIP.  To their credit AIP (which publishes JCP), AAAS (Science), NPG (Nature, Nature Chem) came out and opposed the RWA. Eventually, the ACS also kinda-sorta did but only after the RWA became so unpopular that Elsevier dropped its support (Seriously ACS? After Elsevier? ).

Note also that these societies still charge universities exorbitant prices for their journals (see also this and this) and generate such profits that they are able to shrug off a multimillion dollar loss due to a botched lawsuit against a small rival.

The societies themselves may be not-for-profit outfits, but their publishing divisions certainly are not.

Is the journal open access?  That's a necessary but not sufficient condition.  Consider the BMC journals. Yes, they are OA but they are published by a commercial publisher (Springer) whose mission is to maximise profits.  For example, they are not above selling your figures for profit.  Furthermore, they would not run the OA journal if it did not generate a profit - money they could well use to lobby for the next incarnation of RWA.

That's why I choose PLoS ONE.

How much will it cost?  The nominal charge for publishing a paper in PLoS ONE is $1350, but you can ask for a full or partial fee waiver.  You do this after the paper is accepted.  "The work described in the manuscript is not funded" is a perfectly valid reason for a fee waiver.

Does the journal evaluate papers only on technical soundness? Yes.  In my experience the PLoS ONE review is every bit as rigorous as for other journals and you still have to watch for reviewer comments that ultimately are tied to impact.

Notice that this means you can publish projects that "failed", allowing you to take on riskier projects (remember, that's a good thing!)

Don't go by journal prestige; consider "fit".  PLoS ONE considers manuscripts in all areas of science so all your papers fit perfectly in PLoS ONE.  I find this strangely liberating when planning a research project.

Is there anyone on the editorial board who’d be a good person to handle your paper?  I was initially a little nervous when I didn't see any "friends" on the PLoS ONE editorial board.  However, remember that the editor does not have to judge the perceived "impact" of your work, so who the editor is, is less of an issue than in a conventional journal.

I have had PLoS ONE editors considerably outside my field hand my manuscripts and this has not been an issue so far.

How likely is the journal to send your paper out for external review? PLoS ONE is very likely to send it out for review.

Have you had good experiences with the journal in the past? Yes.

Is the journal part of a review cascade? Not really applicable.

Some additional questions:

So you only publish in PLoS ONE? No, if I think we have a shot at, say, JACS (or even Nature) then I'll give it a shot.  Also, if my co-authors don't want to publish in PLoS ONE then I usually go along with that.  However, I try to insist that the journal allows arXiv deposition so that the some version of the work is freely available.

Isn't PLoS ONE a dump journal? Yes, in the sense that JCTC, JPC, JCP, JCC, etc all are dump journals.  I cannot for the life of me see any meaningful difference in prestige associated with these journals.  If you would rather have a paper in a journal with an impact factor of 5 than one with an IF of 4 then you haven't thought too deeply about what the IF really is.

Will people find your PLoS ONE papers?  Yes, unless their only way of discovering papers is to regularly peruse ToCs of select journals.  However, to reach these people you somehow have to guess which journals that would be and then restrict yourself to solely publishing in those journals. Doesn't this seem a little absurd?


This work is licensed under a Creative Commons Attribution 3.0 Unported License.  

Does publishing in PLoS ONE hurt your chances of getting a PhD? One data point

+Casper Steinmann defends in PhD thesis in a few weeks time.  In Denmark the thesis committee is composed of three people: a local faculty member (not the PhD advisor) and two tenured scientists from other universities, at least one of which must be from outside Denmark.

Prior to the defense the committee writes a brief summary of the thesis and state whether its sufficient for the defense. Most of Casper's PhD research is published in PLoS ONE. Given the online discussion about PLoS ONE going on over at DrugMonkey's blog, I was particularly  happy to see this statement in the report:

Of the five papers (given in Chapters 4 to 9), CS is the first author on four of these. Three of these papers are published in well-renown, high-impact international journals (Journal of Physical Chemistry A (2011), PloS One (2012, 2012), one is submitted to PLoS one and another one will be submitted to The Journal of Chemical Theory and Computation.

Project status: PM6 and PCM in GAMESS

These projects have come up in a couple of emails lately which means it's time to write a blog post.

PM6 in GAMESS
+Jimmy Charnley Kromann is working on implementing PM6 in GAMESS.  It is working for elements up to F.  However, heavier elements require semi-empirical integrals involving d-orbitals which are not in GAMESS.  We have gotten some integral code from James Stewart (who has been a great help in general!) that Jimmy is working on implementing in GAMESS.

The first step is to reproduce PM6 calculations for molecules with non-d-orbitals atoms using the new integral code. As I remember, the 1-electron Hamiltonian is correct, but the 2-electron part of the Fock matrix is still wrong.  It looks like the integrals are computed correctly but indexed wrongly.  Jimmy is busy with classes now but will be back on the case in a few weeks.

Once PM6 is working we also plan to implement DH2 and DH+.

Semiempirical PCM calculations
+Casper Steinmann is spending his vacation working on semiempirical PCM calculations, in particular the implementation suggested by Chudinov et al.  Casper is making great progress so this post will likely be out of date soon and some of the results I refer to are only a few days old.

It looks like the energy calculations are working correctly in the sense that we get very similar solvation energies to Chudinov et al. and RHF/STO-3G calculations.  Gradients have just been implemented but some geometry optimizations fail because the energy changes very little while the maximum gradient is still too large, indicating a numerical problem.  Other geometry optimizations work fine.

The implementation is only for s- and p-functions so far.

Computational efficiency and future directions
Jimmy tested the computational efficiency of PM6 in GAMESS and MOPAC2009 on some large molecules.  An energy + gradient calculation is slower in GAMESS but the geometry optimization converges faster resulting in a overall time savings, but much more testing needs to be done.  We don't know yet how efficient the PCM implementation is yet.

One future goal is to be able to increase the computational efficiency for large molecules such as proteins through a combination of parallelization and fragmentation a la FMO.


This work is licensed under a Creative Commons Attribution 3.0 Unported License.

Blog posts, videos and "other publications" for 2012

Every year I have to fill out several "what have you accomplished last year?" forms.  I've just send in one of them.  There is a section on "other publications", which, I guess, is intended for non-refereed articles and books.  But there are now many other ways to disseminate information so I added:

Blogs
http://molecularmodelingbasics.blogspot.com ca 80,000 pageviews in 2012
http://proteinsandwavefunctions.blogspot.com ca 16,000 pageviews in 2012 (group-blog, includes contributions from others)

Videos
http://www.youtube.com/user/MolModBasics ca 18,000 views i 2012
http://blip.tv/molmodbasics ca 4,000 views i 2012

2012 Presentations
http://www.slideshare.net/molmodbasics/ ca 7,500 views and six downloads i 2012

Proposals
http://figshare.com ca 3,000 views and 34 shares in 2012

Software:
http://propka.org ca 26,000 pageviews in 2012
http://biofetsim.org ca 2,400 pageviews in 2012
http://dgu.ki.ku.dk/molcalc/editor ca 3,500 pageviews in 2012

Like last year, I chose to list views rather than the number of blog posts, videos, or presentations I created in 2012.  I think these numbers are more telling, but I would be happy to hear other suggestions.

It would be interesting to know how many times my papers have been viewed in 2012, but this information is not available for most journals i have published in, and it would be a pain in the neck to collect this data even if it was. 

What I do know is that they have been cited ca 1400 times in 2012 according to Web of Science and that my 2012 papers, which were all in PLoS ONE, were viewed about 1800 times.


This work is licensed under a Creative Commons Attribution 3.0 Unported License.

New Presentation: Blurring the boundary between linear scaling QM, QM/MM and polarizable force fields

Here are my slides for a talk I will give in Tromsø on Monday.  I am talking about +Casper Steinmann's EFMO method.

Blurring the boundary between linear scaling QM, QM/MM and polarizable force fields from molmodbasics

This work is licensed under a Creative Commons Attribution 3.0 Unported License.

Using Molecular Overlap to Select Approximations in the Fragment Molecular Orbital Method

A former student (who did the initial work) and I investigated here whether using overlaps between fragments to select the appropriate form of approximation in the Fragment Molecular Orbital method was any good. While not a complete manuscript in any form yet, the work-in-progress will be updated here to reflect new tendencies. In the end, it should be submitted to arXiv and eventually a peer-reviewed publication.

Here is the outline of what would be the paper - sprinkled with some text here and there along with a long list of TODO's.

1 Introduction

Until now, every fragment based method which aims to be linearly scaling needs approximations for largely separated n-mers. These approximations are invoked based on distances which are empirically determined to give results which are good enough but still ensure that the method scales linearly. This rather blunt instrument leaves much to be desired

2 Background and Theory

2.1 Relevant FMO equations

In the FMO method, the total energy of a system of $N$ fragments (monomers) is given as

$$E = \sum_I E_I + \sum_{I>J}^{close} \Delta E_{IJ} + \sum_{I>J}^{separated} \Delta \tilde{E}_{IJ} + \sum_{I>J>K}^{close} \Delta E_{IJK}.$$

Here, $E_I$ is the energy of monomer $I$ evaluated in the ESP of all other fragments. Pairs $IJ$ (dimers) are evaluated based on the shortest interfragment monomer distance $R_{I,J}$ (see (Steinmann2010effective) for definition). Dimers in close proximity ($R_{I,J} < R_\mathrm{resdim} $ where $R_\mathrm{resdim}$ is a user-defined distance) are evaluated self-consistently in the fixed ESP of the monomers

$$\Delta E_{IJ} = E_{IJ} - E_I - E_J.$$

Here, $E_{IJ}$ is the energy of dimer $IJ$ made from monomers $I$ and $J$. Separated dimers ($R_{I,J} > R_\mathrm{resdim} $) are evaluated using a Coulomb expression

$$\Delta \tilde{E}_{IJ} = \mathrm{Tr}(\mathcal{D}^Iu^J) + \mathrm{Tr}(\mathcal{D}^Ju^I) + \sum\sum \mathcal{D}^I\mathcal{D}^J(\mu\nu|\lambda\sigma) + \Delta E^\mathrm{NR}_{IJ},$$

where $\mathcal{D}^I$ is the density of monomer $I$, $u^J$ is the potential from the nuclei of fragment $J$ and $\Delta E^\mathrm{NR}_{IJ}$ is the nuclear repulsion interaction between nuclei in $I$ and $J$. The final term in Eq.1 is the trimer correction for trimer $IJK$. It is evaluated self-consistently only for close trimers (see [fedorov2004importance] for definition) in the fixed ESP of all monomers and given as

$$\Delta E_{IJK} = E_{IJK} - E_I - E_J - E_K - \Delta E_{IJ} - \Delta E_{IK} - \Delta E_{JK}.$$

Here, $E_{IJK}$ is the energy of trimer $IJK$. There is no corresponding approximate expression for trimer energies as in Eq. 3.

The default values for the distance based cutoffs for dimers and trimers are empirically determined to provide a reasonable mix of dimers and trimers with fortuitous error cancellation. We do note that the original formulation for the FMO3 method, no approximated dimers enter the equation due to the way the thresholds are set up. However as the number of trimers increases rapidly with system size it becomes unfeasible for large systems to carry out an FMO3 single point energy calculation. We propose an additional cutoff besides the distance cutoff based on the maximum overlap between dimers within a distance of $R_\mathrm{resdim}$ of each other. This helps to remove those $n$-mers that contribute little to the total energy with a noticeable speedup in computational effort.

2.2 Approximate Overlap Matrix

In this new approach, we want to calculate the maximum in the overlap matrix

$$\max_{i\in I,j\in J}\left\{S_{ij}\right\},$$

between two monomers $I$ and $J$ which make up dimer $IJ$ and use that overlap to determine whether we can ignore an SCF calculation on that dimer. Here $i$ and $j$ refer to MOs. Traditionally this requires the following transformation from atomic orbitals (AO)

$$S_{ij} = \langle \psi_i | \psi_j \rangle = \sum_i^\mathrm{occ} \sum_j^\mathrm{occ} C_{IJ,i\mu} C_{IJ,j\nu} \langle \chi_\mu | \chi_\nu \rangle = \sum_i^\mathrm{occ} \sum_j^\mathrm{occ} C_{IJ,i\mu} C_{IJ,j\nu} S_{\mu\nu},$$

where the matrices $\mathbf{C}_{IJ}$ are MO coefficient matrices for dimer $IJ$, $\chi_\mu$ is an atomic orbital and $S_{\mu\nu}$ is the overlap matrix in AO basis. However, this requires the full SCF calculation to already have been carried out on dimer $IJ$. Instead, we choose to approximate the dimer MOs by combining monomer MOs

$$C_{IJ} \approx C_I \oplus C_J.$$

Using the above, we can now calculate the maximum overlap (Eq.~\ref{eqn:maxoverlap}) through the transformation (Eq.5) \emph{before} we evaluate the SCF of the dimer. This enables us to do an approximate dimer (Eq.3) if the overlap is not large enough.

2.3 Considerations for Dimers and Trimers

2.4 Implementation and Methodology

The overlap based rejection of dimers and trimers was implemented in a locally modified version of GAMESS using the distributed data interface [25]. For all calculations SCF convergence was increased (\$CONV=1E-7 in \$SCF) to match that of FMO and integral accuracy increased (ICUT=12 in \$CONTRL).

For all FMO calculations we used the default values for cutoffs based on distances (RESDIM=2.0 in \$FMO for dimers, RITRIM(1)=1.24, -1.0, 2.0, 2.0 in \$FMO for trimers). To obtain approximate dimer MO coefficients we used MODORB=3 in $FMOPRP. All other setting were default value unless specified directly.

3 Results 

TODO: Compile the results and write about them. Benchmarking water clusters from previous FMO applications should be OK.

TODO: There is a problem with the test-systems of the ALA-helices and sheets, perhaps it is because they are too simple and repetitive to actually mean anything

3.1 Overlap vs. Distance

3.2 Dimers 

3.3 Trimers

4 Conclusion and Outlook

1) there is a noticeble difference between using basis sets with and without diffuse functions

2) works great for molecular clusters, systems with covalent bonds??

Generating an Orthonormal Basis

So you have a vector $\mathbf{V}_1=(V_x, V_y, V_z)$ and you want to construct an orthonormal basis with that one vector as one of the basis vectors. $\mathbf{V}_1$ is not normalized, yet. Here is how I did it, first concentrating on providing the orthogonal set of vectors

The Orthogonal Basis

The first orthorgonal vector to $\mathbf{V}_1$, called $\mathbf{V}_1$ is done by
$$
\mathbf{V}_2=(-V_y, V_x, 0).
$$
We can easily verify that $\mathbf{V}_1$ and $\mathbf{V}_2$ are orthogonal by taking the inner product
$$
\langle\mathbf{V}_1,\mathbf{V}_2\rangle = V_x\cdot(-V_y)+V_y\cdot V_x + V_z\cdot 0 = -V_xV_y+V_xV_y = 0.
$$
The last orthogonal vector $\mathbf{V}_3$ is created by taking the cross-product of $\mathbf{V}_1$ and $\mathbf{V}_2$ yielding
$$
\mathbf{V}_3=\mathbf{V}_1\times\mathbf{V}_2=(V_y\cdot 0 - V_z\cdot V_x,V_z\cdot (-V_y)-V_x\cdot 0,V_x\cdot V_x - V_y\cdot (-V_y)),
$$
and can be reduced to

$$
\mathbf{V}_3=(-V_x\cdot V_z, -V_y\cdot V_z, V^2_x+V^2_y).
$$
Thus $\mathbf{V}_1$, $\mathbf{V}_2$ and $\mathbf{V}_3$ now constitue an orthogonal basis. However, normalizing by brute-force is cumbersome (and error prone) so we will take a slightly more clever route.

The Orthonormal Basis

If we instead assume that the vector $\mathbf{V}_1$ is normalized initially, we have that
$$
\hat{\mathbf{V}}_1 = (V_x, V_y, V_z).
$$
I've re-used the same symbols as before to reduce an unnecessary cluttering of the notation, but do remember that elements of $\hat{\mathbf{V}}_1$ are normalized. To help us later on, we can write the length of $\hat{\mathbf{V}}_1$ as
$$
1=\sqrt{V^2_x + V^2_y + V^2_z}=> 1=V^2_x + V^2_y + V^2_z
$$
which we will use momentarily. $\hat{\mathbf{V}}_2$ is constructed as above but we have to normalize right away

$$
\hat{\mathbf{V}}_2 = (\frac{-V_y}{\sqrt{V^2_x + V^2_y}}, \frac{V_x}{\sqrt{V^2_x + V^2_y}}, 0)=(\frac{-V_y}{\sqrt{1-V^2_z}}, \frac{V_x}{\sqrt{1-V^2_z}}, 0)
$$
In the final equality sign, we used the length of $\hat{\mathbf{V}}_1$.

Now, for the cross-product. Remember that the no normalization for $\hat{\mathbf{V}}_3$ is needed because $\hat{\mathbf{V}}_1$ and $\hat{\mathbf{V}}_2$ are already normalized

$$
\hat{\mathbf{V}}_3=\hat{\mathbf{V}}_1\times\hat{\mathbf{V}}_2=(\frac{-V_z\cdot V_x}{\sqrt{1-V^2_z}},\frac{-V_z\cdot V_y}{\sqrt{1-V^2_z}},\frac{V^2_x+V^2_y}{\sqrt{1-V^2_z}}).
$$

The last element of the $\hat{\mathbf{V}}_3$ vector is something we can take care of and make it a tad prettier. By using the length of vector $\hat{\mathbf{V}}_1$ again we obtain

$$
\hat{\mathbf{V}}_3=(\frac{-V_z\cdot V_x}{\sqrt{1-V^2_z}},\frac{-V_z\cdot V_y}{\sqrt{1-V^2_z}},\frac{1-V^2_z}{\sqrt{1-V^2_z}}),
$$

and if we remember that $x/\sqrt(x)=\sqrt(x)$ we finally obtain $\hat{\mathbf{V}}_3$ as

$$
\hat{\mathbf{V}}_3=(\frac{-V_z\cdot V_x}{\sqrt{1-V^2_z}},\frac{-V_z\cdot V_y}{\sqrt{1-V^2_z}},\sqrt{1-V^2_z}).
$$

So to sum up, given a normalized vector $\hat{\mathbf{V}}_1$, we can construct an orthonormal basis using the following equations

$$
\hat{\mathbf{V}}_1 = (V_x, V_y, V_z),
$$
$$
\hat{\mathbf{V}}_2 =(\frac{-V_y}{\sqrt{1-V^2_z}}, \frac{V_x}{\sqrt{1-V^2_z}}, 0),
$$
$$
\hat{\mathbf{V}}_3=(\frac{-V_z\cdot V_x}{\sqrt{1-V^2_z}},\frac{-V_z\cdot V_y}{\sqrt{1-V^2_z}},\sqrt{1-V^2_z}).
$$

The clever thing about these last expressions is that the normalization factor $\sqrt{1-V^2_z}$ is present many times and can be precomputed for each new $\hat{\mathbf{V}}_1$.


Acknowledgements: Thanks to Lars for being awesome with the math.

Manuscript review: Mapping Enzymatic Catalysis using the Effective Fragment Molecular Orbital Method: Towards all ab initio Biochemistry

+Casper Steinmann's latest paper, which he submitted to PLoS ONE late last month, has already been reviewed!  Way to go PLoS ONE!

Points 1-6 are easily addressed.

7. cc-pVTZ single points on one representative path should be no problem, even with MP2.  If we see only a small change in barrier I would argue against cc-pVQZ calculations.  Otherwise, we should at least do the B3LYP/cc-pVQZ calculations on the same path.

8. I don't quite follow the line and page number reference.  But we use a smaller model than
Claeyssens et al.: all atoms with 16 Å and 25 Å of the active site, respectively.  So the enzyme model is poorer.

9. Of course the reaction enthalpy in the enzyme cannot be measured, only estimated, so it's not a good benchmark.  Nevertheless, Claeyssens et al. estimate the "experimental" enzymatic reaction enthalpy to be between -15 and -13 kcal/mol. Our best prediction of the reaction enthalpy is about -6 kcal/mol (Figure 6).  Reference 37 predicts between -26 and -36 kcal/mol (and Claeyssens et al. -18.2$\pm$1.3 kcal/mol).  Clearly the predictions differ greatly, but the problem seems to lie more with the method described in reference 37.

10. I think that should actually be 5.4 kcal/mol (27.6-22.2) instead of 8.  Anyway, the main change is the inclusion of enzyme-substrate dispersion interactions, which must be weaker in the TS compared to the reactant.  It is not clear whether the largest effect is on the H-bonds to the substrate or a many small contributions from all the atoms in the blue and red region in Figure 4.  Additional calculations would be required, I don't think it's worth it.

11. Claeyssens et al. (reference 40 in our paper) computed the barrier with B3LYP/6-31G(d).

12. As we write on page 10: our barrier is 18.3$\pm$3.6 kcal/mol and Claeyssens et al.'s barrier is 9.7$\pm$1.8 kcal/mol.

13. As mentioned on page 10: The experimental activation enthalpy is 12.7$\pm$0.4 kcal/mol.  So Claeyssens et al.'s error is 3.0 kcal/mol and our error is 5.5 kcal/mol. The multilayer barrier represents just one MD snapshot.

14. This has been addressed in point 9.

From: PLOS ONE <plosone@plos.org>
Date: 14. jan. 2013 20.56.05 CET
To: Casper Steinmann <xxx>
Subject: PLOS ONE Decision: Revise [PONE-D-12-39084]

PONE-D-12-39084
Mapping Enzymatic Catalysis using the Effective Fragment Molecular Orbital Method: towards all ab initio Biochemistry
PLOS ONE

Dear Mr Steinmann,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit, but is not suitable for publication as it currently stands. Therefore, my decision is "Major Revision."

We invite you to submit a revised version of the manuscript that addresses the points below:

There are some minor issues listed below, but one primary problem that must be addressed with additional text and possibly the single point calculations that the referee refers to in point 7. The serious energy discrepancy must be addressed as amply discussed by the reviewer.
We encourage you to submit your revision within forty-five days of the date of this decision.

When your files are ready, please submit your revision by logging on tohttp://pone.edmgr.com/ and following the Submissions Needing Revision link. Do not submit a revised manuscript as a new submission. Before uploading, you should proofread your manuscript very closely for mistakes and grammatical errors. Should your manuscript be accepted for publication, you may not have another chance to make corrections as we do not offer pre-publication proofs.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter.

Please also include a rebuttal letter that responds to each point brought up by the academic editor and reviewer(s). This letter should be uploaded as a Response to Reviewers file.

In addition, please provide a marked-up copy of the changes made from the previous article file as a Manuscript with Tracked Changes file. This can be done using 'track changes' in programs such as MS Word and/or highlighting any changes in the new document.

If you choose not to submit a revision, please notify us.

Yours sincerely,

xxxx
Academic Editor
PLOS ONE

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Yes

---

Please explain (optional).

Reviewer #1: (No Response)

---

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

---

Please explain (optional).

Reviewer #1: (No Response)

---

3. Does the manuscript adhere to standards in this field for data availability?

Authors must follow field-specific standards for data deposition in publicly available resources and should include accession numbers in the manuscript when relevant. The manuscript should explain what steps have been taken to make data available, particularly in cases where the data cannot be publicly deposited.

Reviewer #1: Yes

---

Please explain (optional).

Reviewer #1: (No Response)

---

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors below.

Reviewer #1: Yes

---

Please explain (optional).

Reviewer #1: (No Response)

---

5. Additional Comments to the Author (optional)

Please offer any additional comments here, including concerns about dual publicationor research or publication ethics.

Reviewer #1: This paper describes the implementation and first tests of the frozen-domain approximation for the effective fragment molecular orbital method for the chorismate mutase enzyme reaction. The calculations are carefully tested and well done. The results are interesting and therefore publishable. However, compared to previous calculations, the approach shows very large deviations in some energies. These need to be explained before the method can be trusted (points 9 and 10).
1. The level of EFMO should be specified in the abstract.
2. It should be shortly discussed how dangling bonds in the QM calculations are treated.
3. The protonation of all residues should be specified, in particular for the His residues. The number of counter ions and their nature (what element?) should also be specified.
4. I suppose Bohr should also be written with a capital B.
5. The legend of Figure 3 should point out that C1 and C5 is the shared atom.
6. I suppose the references to Figure 2 on p. 6 are misprints (should be Figures 4 and 5).
7. Single-point calculations should also be performed for isolated chorismate with TZP and QZP basis sets, both at B3LYP and MP2 levels of theory, to check the basis set effects.
8. Line -5 on p. 9: Is the enzyme model poorer in the present or the previous study?
9. The ~30 kcal/mol difference in the reaction energy between the present results and those in refs 36 and 37 is very alarming. It sounds unlikely that this should be caused by the restricted relaxation in this study (the large model changes the energy by only 3 kcal). This difference must be better explained. How could the authors expect that we should trust a method that can give errors of 30 kcal?
10. Why do the multilayer calculations give so different results (8 kcal) compared to the ONIOM calculations? Which approach is best? Again, this large difference is very alarming and reduces the credibility of the present approach.
11. Still another reason for the difference between the present results and that by Claeyssens et al. is of course the use of LCCSD(T0) with large basis sets in the latter study.
12. Is the energy spread among the 7 snapshots similar or larger than in previous studies?
13. I cannot see that a doubling of the computational cost is a big problem. On the other hand, in my eyes a method that gives errors of 30 kcal, or even 8 kcal is completely useless. The authors should think more on the accuracy than on the timing.
14. Is the reaction enthalpy experimentally known? It seems to be harder to estimate than the activation enthalpy and therefore more interesting to study and reproduce.

---

6. If you would like your identity to be revealed to the authors, please include your name here (optional).

Your name and review will not be published with the manuscript.

Reviewer #1: (No Response)

Summary of select research projects

Summary of Select Research Project (Early 2013) from molmodbasics

Yesterday I made a presentation at at group meeting of the Stamou Group and briefly described three projects that might be of interest to them: projects by +Casper Steinmann, +Anders Steen Christensen, and +Martin Hediger  


This work is licensed under a Creative Commons Attribution 3.0 Unported License.

Negative temperature: the equations

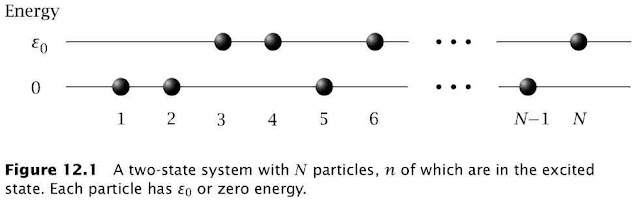
A recent Science paper entitled Negative Absolute Temperature for Motional Degrees of Freedom has generated a lot of discussion on the blogosphere (example) already.  This post is about the equations behind the concept of negative temperature.  The discussion and figure is taken out of chapter 12 of the excellent book Thermodynamic Driving Forces by Dill and Bromberg.

The thermodynamic definition of temperature is
$$dS=\frac{dU}{T}=\left(\frac{dS}{dU}\right)_{V,N}dU\Rightarrow\frac{1}{T}=\left(\frac{dS}{dU}\right)_{V,N}$$while the statistical mechanical definition of entropy is $$S=k\ln(W)$$

For a two-state system (Figure 12.1)$$\frac{1}{T}=k\left(\frac{d\ln(W)}{dn}\right)_{V,N} \left(\frac{dn}{dU}\right)$$The multiplicity term can be rewritten as $$\ln(W)=\ln\left(\frac{N!}{n!(N-n)!}\right)\approx-n\ln\left(\frac{n}{N}\right)-(N-n)\ln\left(\frac{N-n}{N}\right)$$where the last term used Stirling's approximation $x!\approx (x/e)^x$. The internal energy is given by$$U=n\varepsilon_0\Rightarrow\frac{dn}{dU}=\frac{1}{\varepsilon_0}$$so $T$ can be defined in terms of the fraction of molecules in the ground $(f_{ground}=n/N)$ and excited state $(f_{excited}=1-n/N)$ $$\frac{1}{T}=\frac{k}{\varepsilon_0}\ln\left(\frac{f_{ground}}{f_{excited}}\right) $$At equilibrium these fractions are determined by the Boltzmann distribution$$\frac{f_{ground}}{f_{excited}}=e^{\varepsilon_0/kT}>1$$This is the $T$ you measure with a thermometer and this $T$ can never be negative at equilibrium.  However, if you create a excited macrostate for which $f_{ground}/f_{excited}<1$ then the corresponding variable $T$ can indeed be negative.  As pointed out by Michael de Podesta this happens all the time in a laser.



This work (except the first figure which is © by Garland Science) is licensed under a Creative Commons Attribution 3.0 Unported License.

Journal of Molecular Modeling considers manuscripts deposited on arXiv

From: Jan Halborg Jensen
Sent: Thursday, January 03, 2013 2:22 PM
To: Journal of Molecular Modeling
Subject: Re: Manuscript JMMO-D-12-xxx for review

Dear xxx

Happy new year!

Does JMMO consider paper that have been deposited on the preprint server arXiv?  I ask because I am boycotting (i.e. not reviewing for or submitting to) all journals that don't.

Best regards, Jan

----

From: xxx

Sent: Friday, January 04, 2013 9:02 AM

To: Jan Halborg Jensen; xxx

Subject: JMM

Dear Jan,

I confirm that JMM consider archived papers.

Regards.

xx

----

From: Jan Halborg Jensen
Sent: Friday, January 04, 2013 10:28 AM
To: xxx
Subject: Re: JMM

Dear xxx

Excellent!  Then I'd be happy to review the paper.

Best regards, Jan

This work is licensed under a Creative Commons Attribution 3.0 Unported License.

Manuscript in progress: Protein structure validation and refinement using amide proton chemical shifts derived from quantum mechanics

+Anders Steen Christensen and I are working on the first draft of this manuscript.  Here is the story as I see it now (stay tuned for updates).

The ProCS method
We introduce the QM-based ProCS method for predicting backbone amide proton chemical shifts given a protein structure.  It is a generalization and improvement of a method I published earlier.

Reproducing QM chemical shifts
ProCS is parameterized based on B3LYP/6-311++G(d,p)//B3LYP/6-31+G(d) calculations. This level of theory has been shown to yield reliable proton chemical shifts (how reliable for small molecules). ProCS involves several terms from backbone dihedral angles, hydrogen bonding, etc. with an additivity assumption.  If everything works perfectly we should be able to reproduce B3LYP/6-311++G(d,p)//B3LYP/6-31+G(d) chemical shifts for a protein structure.

Anders has computed the B3LYP/6-311G(d,p)/PCM chemical shielding tensors for the 1ET1 x-ray structure.  (The lack of diffuse functions is taken care of by scaling factor from literature). ProCS can reproduce QM with an RMSD of 0.37 ppm.  Remaining deviation must come from non-additivity.

The empirical methods do not agree well with the DFT results.  The DFT CSs span a relatively large range while the empirically predicted CSs span a very short range.  This indicates that the empirical methods are less sensitive to small differences in hydrogen bond geometry.

Reproducing experimental chemical shifts from X-ray structures
QM reproduces small molecule H1-CSs with RMSD of xx.  However, for 1ET1 the RMSD is yy.  The main source of the discrepancy are likely inaccuracies in the x-ray structure HB-bond lengths since there is an exponential dependence.  

The PROCS RMSD (0.63) is similar to the QM RMSD(??), and significantly larger than the RMSD between QM and ProCS, indicating that ProCS sufficiently accurate.  Going to 13 other proteins the RMSD for ProCS is double that of 1ET1, because more amide protons not involved in HBs.

The RMSDs for the empirical methods are significantly smaller than ProCS.  This is also found for 13 other X-ray structures.  This is because the empirical methods are parameterized using x-ray structures.  In order for these methods to produce low RMSD relative to experiment they need to be insensitive to errors in protein structure.


Monte-Carlo implementation of protein structure refinement based on chemical shifts
Why MC?  No gradients for ProCS.  More efficient sampling based on Bayesian inference.  Anything else?

Refining protein structures based on chemical shifts

We refine the structure of three proteins each based on three energy function: OPLS alone, OPLS+ProCS and OPLS+Camshift.  The MC-refinement of a protein structure results in an ensemble of X (?) protein structures from which average chemical shifts for each amide proton are computed.

These average ProCS chemical shifts are in better agreement with experiment compared to using x-ray.  The  hydrogen bond geometries in the ensemble are very close to the x-ray structures.  These average Camshift chemical shifts are in not in better agreement with experiment compared to using x-ray.  The  hydrogen bond geometries in the ensemble are longer than in the x-ray structures.  This is because OPLS prefers longer bond lengths.

Trans-hydrogen bond coupling constants

Better agreement with x-ray structures does nto necessarily imply better solution-phase structures, so we computed average trans-hydrogen bond coupling constants and compared to experiment.  The coupling constants based on the Pro-CS refined ensembles are indeed in better agreement with experimental values indicating the refinement led to improved hydrogen bond geometries

Summary

ProCS is a QM-based backbone amide proton chemical shift predictor that can deliver QM quality CS predictions for a protein structure in less than a second.  Agreement with experiment is worse compared to empirically predicted CS, but we show that this is because empirical CS predictors are insensitive to small errors in hydrogen bond geometry in the x-ray structures.  This is because they are parameterized using such x-ray structures.   The agreement between ProCS CSs and experiment can be improved by refining the protein structure using an energy function that includes a force field term and a CS term.  This also results in better predicted trans-hydrogen bond coupling constants indicating that the refined protein structures indeed have improved.  A similar refinement using Camshift CS lead to worse protein structure by the same criterion.  

Empirical CS-predictors result CSs that agree better with experiment.  However, they are relatively insensitive to protein structure and are therefore not suitable for protein structure refinement.

This work is licensed under a Creative Commons Attribution 3.0 Unported License. 

The enthalpy increases when bonds are broken

Enthalpy changes comes mainly from changes in bonding
An enthalpy change has four contributions$$\Delta H^\circ=\Delta E^{Molecular}+\Delta H^{\circ,Translation}+\Delta H^{Rotation}+\Delta H^{Vibration}$$The molecular energy $\Delta E^{Molecular}$ is associated with the electrons and nuclei, i.e. chemical and intermolecular bonding, and this is often the largest term.

For example for the reaction $H_2 \rightarrow 2H$ the enthalpy contributions are:$$\Delta H^\circ = 460.2+6.3-2.5-26.4=437.6 \text{ kJ/mol}$$For breaking the hydrogen bond between two water molecules,$H_2O\cdot \cdot \cdot HOH\rightarrow 2H_2O$, the energy terms are$$\Delta H^\circ = 20.5+6.3+3.8-17.6=13.0 \text{ kJ/mol}$$In both cases $\Delta H^\circ$ is positive mainly because it requires energy to break a covalent bond or a hydrogen bond.

Figure 1. The attraction between partially charged atoms in a hydrogen bond is contained in $\Delta E^{Molecular}$ [image source]

Estimating enthalpy changes of chemical reactions
Most chemical reactions are not as simple as $H_2 \rightarrow 2H$ and involve the making and breaking of several bonds.  For example for this reaction there are three double bonds and one single bond in the reactant molecules and one double bond and five single bonds in the product molecule.

Figure 2. The prototypical Diels-Alder reaction where 1,3-butadiene reacts with ethene to form cylcohexene 

To estimate the enthalpy change this reaction you need to know the strengths of CC double and single bonds which are 611 and 347 kJ/mol respectively.  So it requires $3\times 611+347=2180$ kJ/mol to break the bonds in the reactants and you get back $-(611+5\times 347)=-2346$ kJ/mol back when you form the bonds in the products, so $\Delta H^\circ=-166$ kJ/mol is a good estimate of the enthalpy change.

You can find a list of bond strengths here.  The values are given in kcal/mol so you must multiply them by 4.184 to convert to kJ/mol.

Enthalpies of formation
Enthalpies of formation ($\Delta H^\circ_f$, also called heats of formation) can also be used to  estimate $\Delta H^\circ$ for a reaction.  So for the reaction in Figure 2:$$\Delta H^\circ=\Delta H^\circ_f(\text{cyclobutene})-\Delta H^\circ_f(\text{1,3-butadiene})-\Delta H^\circ_f(\text{ethene})$$ You can find enthalpies of formation of many molecules on the web by Googling or you can estimate them using the Molecule Calculator.

Endothermic and exothermic reactions
Reactions for which the enthalpy increases are called endothermic reactions and reactions for which the enthalpy decreases are called exothermic

Test: Is this an endo- or exothermic process?

    

This work is licensed under a Creative Commons Attribution 3.0 Unported License.